Chaos theory and complex systems have their own characteristics, words and concepts, without which it is not possible to properly interpret their use in the study of a phenomenon. In the following, I will describe some of the most important features and concepts related to chaos theory and complex systems. In this article, you will get acquainted with the concept of fractal.
In the 1980s, Benoit Mandelbrot used his home computer for what he called a fractal. A fractal is a self-similar shape in which a basic shape is repeated continuously and at different levels. For example, if you look at ferns, you will see that the sub-branches in the branches of the fern tree are similar to the whole tree, and the sub-branches of the tree branches have repeated the same structure, this is the basic shape of the same fractal.

Self-Similar Structure in Fern Tree
Fractals are unexpected patterns of order in chaos, all of which have similar properties. A self-similar system has a fixed pattern that is repeated at different levels. For example, if you look at a picture of desert sand, you can not guess whether your field of view is 5 meters or 500 meters, these pictures can be very close or very far. The base shape of the sand pile is similar at all distances. This is called “self-similarity” or “scale-free”.
The shape of fractals at different levels of perspective is similar to itself, but look at them on any scale, you will see the same appearance. In the image of desert sands, you can only recognize the scale when, for example, there are several camels in the image. You can also imagine an image of a beetle walking on desert sands, which shows the scale of your image.

Sand Image (Scale is not Recognizable)

The Same Image but With Addition of Few Camels (Scale is Recognizable)
In 1975, Benoit Mandelbrot, a mathematician working for IBM, used the term fractal to describe self-similar patterns. In 1967, he posed a question and a challenge. The question was, what is the length of the British coastline (how many kilometers)? At first glance, the answer to this question may seem simple. But it is very difficult to calculate. It may be thought that by measuring a scale and placing it on a British map, one can calculate the size and ultimately the length of the British coast. But if we have a more detailed map, we will find that there are many small bays and coastlines that are not shown on larger-scale maps.
This causes the shoreline to increase. If we even want to calculate the exact size, we will find that the length of the shoreline increases again. So, if you think about it right, the length of the shoreline that we calculate depends on how we calculate, and the more accurately we calculate, the longer the shoreline increases. Finally, the length of the shoreline is indeed infinite. If you look at the map, you can not tell if you are looking at a kilometer from the shoreline or a thousand kilometers. In fact, the shoreline has a fractal structure.
No matter how much you look at the map at high magnification, the original shape of the map remains fixed. The lines shown on the map can be blocks of agricultural land or the borders of interstate countries, such as South America.
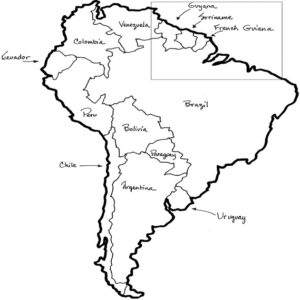
Map of South America and its Fractal Structure
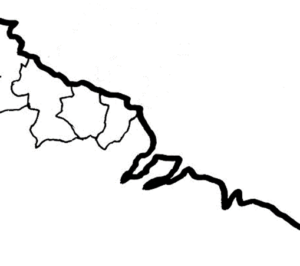
Coastal and Northern Line of the Above Map, Which on a Larger Scale Can be Considered a Map of Other Countries (ie Map on the Map)
The trees themselves are self-similar. A small branch of a tree has the basic shape of the whole tree. If you consider the English letter (Y) and repeat the same letter Y in each of the above branches and do this for several steps, you will end up with a tree-like shape. The nature around us is full of fractals. Fractal shapes can also be found in cabbage or broccoli. Our body organs are also filled with fractal structures. The shape of the airways in the human lungs is actually based on the fractal inverted letter (Y). The kidneys, blood vessels, and even neural networks in the human brain are based on fractal shapes.
Fractal Structure in Human Lungs
Fractals found in nature, like fractals made with mathematical formulas, are not perfect and do not repeat infinitely at magnification levels. In nature, a total of seven levels of fractal patterns are found, and after these seven levels, the fractal size becomes so small that it is no longer recognizable. Fractals are not only found in the natural world, but also in the man-made world. If you look at a map of a city, you will see a similar structure. For example, you can see highways, from which the roads are branched out in a series, and from the same roads, streets are branched, and from the streets, alleys are branched.

Fractal Structure in Cities
It may be easier for us Iranians to understand fractals than other peoples. Because we have played on Iranian carpets and rugs since childhood, and the pattern of most carpets and rugs is composed of repeating different geometric and non-geometric shapes at different levels. These shapes are exactly the fractals that make up the great design of carpets and rugs.

Fractals in Carpets
Interestingly, fractals can be defined even in abstract and conceptual issues. For example, how a rumor spreads in a community or even forms a strategic logic in the culture of an organization or system has a fractal structure. Stories, narratives, proverbs and even images can be developed as a fractal in the intellectual space of a society or organization, repeated at different levels and expanded.
The question is, why has nature used fractal patterns in so many structures? Natural selection tends to select structures with the lowest efficiency to remove, and over time only the structures with the highest efficiency remain. In our lungs, the airway structures are distributed in such a way that they are most efficient at delivering oxygen to the bloodstream. In a fractal pattern, such as the air ducts in the lungs, the diameter of the ducts in each fractal (at the point of branching) is reduced so that the reduction ratio is constant in all branches and also provides the highest coefficient of air penetration into the bloodstream through these ducts.



How a fire spreads in a field or forest, the structure of lightning, a certain type of cabbage also have a fractal structure. Even the structure of galaxies and star systems have a fractal structure. Interestingly, Professor Mahmood Hesabi developed a theory that believed that every particle was infinitely wide and scattered throughout space. In this view, all the particles of the universe are interconnected. Because it is assumed that every particle is infinitely wide and all the particles of the universe exist together in different parts of the world. That is, there is a small part of the whole world anywhere. In general, fractals range from infinitesimal quantum particles to galaxies and supernovae. In more general terms, fractals are the mechanism by which God created the universe.

 فارسی
فارسی